Link to Advent of Code day 17

Today's problem was fun, even if it involved playing with a 2d grid again. The solution was a simple path-finding algorithm, but I like them so that's ok.

Part 1

Rules

Today's problem is that we have to push crucibles from one point to another, while minimizing the heat loss on the way.

The input is a map of the heat loss which occurs on each tile:

2413432311323
3215453535623
3255245654254
3446585845452
4546657867536
1438598798454
4457876987766
3637877979653
4654967986887
4564679986453
1224686865563
2546548887735
4322674655533

The starting point is the top left tile, and we must reach the bottom right tile, picking the path with the less heat loss.

The constraints are the following:

1. We can move at most 3 tiles in the same direction
2. We can only turn 90 degrees left or right

We need to find how much heat loss would occur with the optimal path.

Code

The easiest solution to find the path with the least heat loss is to consider the map as a weighted graph, and to implement a Dijkstra's algorithm.

Let's start by implementing a node in this graph:

from copy import copy
from dataclasses import dataclass
from enum import Enum


class Direction(Enum):
    NORTH = (-1, 0)
    EAST = (0, 1)
    SOUTH = (1, 0)
    WEST = (0, -1)


@dataclass
class Node:
    # The position of this node on the map
    y: int
    x: int
    # How many steps is remaining before having to turn
    remaining_steps: int
    # The direction of this node on the map
    direction: Direction

    def copy(self):
        return copy(self)

    def move(self):
        y_delta, x_delta = self.direction.value
        self.y += y_delta
        self.x += x_delta
        self.remaining_steps -= 1

    def turn_left(self):
        self.direction = {
            Direction.NORTH: Direction.WEST,
            Direction.EAST: Direction.NORTH,
            Direction.SOUTH: Direction.EAST,
            Direction.WEST: Direction.SOUTH,
        }[self.direction]
        self.remaining_steps = 3

    def turn_right(self):
        self.direction = {
            Direction.NORTH: Direction.EAST,
            Direction.EAST: Direction.SOUTH,
            Direction.SOUTH: Direction.WEST,
            Direction.WEST: Direction.NORTH,
        }[self.direction]
        self.remaining_steps = 3

    def __hash__(self):
        return hash((self.y, self.x, self.remaining_steps, self.direction))

    def __lt__(self, other):
        return (self.remaining_steps, self.y, self.x) < (other.remaining_steps, other.y, other.x)

You can see that I borrowed a lot from day 16 for the direction and rotation. I added a implementation of __lt__ which will be required for the usage of heapq in the Dijkstra implementation later.

The nodes are handled by the class Graph, which will contain the map of heat loss, and provide the possible states which are possible from a given node:

class Graph:
    def __init__(self, crucibles: list[list[int]]):
        self.crucibles: list[list[int]] = crucibles
        self.width = len(crucibles[0])
        self.height = len(crucibles)

    def get_neighbors(self, node: Node):
        """ Generate each direct possible state, and the associated heat
         loss for each state, from a given node.
        """
        yield from self.advance(node)

        left_node = node.copy()
        left_node.turn_left()
        yield from self.advance(left_node)

        right_node = node.copy()
        right_node.turn_right()
        yield from self.advance(right_node)

    def advance(self, node: Node):
        """ Generate each state a node can have by moving in a straight line,
        and the heat loss induced by the movement.
        """
        if node.remaining_steps <= 0:
            return

        tmp_node = node.copy()
        weight = 0
        while tmp_node.remaining_steps > 0:
            tmp_node = tmp_node.copy()
            tmp_node.move()
            if self.out_of_map(tmp_node):
                return
            weight += self.crucibles[tmp_node.y][tmp_node.x]
            yield tmp_node, weight

    def out_of_map(self, node: Node) -> bool:
        return node.y < 0 or node.x < 0 or node.y >= self.height or node.x >= self.width

You can see this party is a bit messy, I'll try to fix it in part 2. Once we have the node and the graph, we have all we need to implement a dijkstra:

import heapq
from collections import defaultdict


def dijkstra(graph: Graph, start: Node):
    distances = defaultdict(lambda: float("inf"))
    distances[start] = 0
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_vertex = heapq.heappop(priority_queue)

        if current_distance > distances[current_vertex]:
            continue

        for neighbor, weight in graph.get_neighbors(current_vertex):
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))

            if (neighbor.x == graph.width - 1) and (neighbor.y == graph.height - 1):
                return distances, neighbor

    raise ValueError("No solution found for the given graph")

Nothing super fancy here, it's the classic implementation.

Since we only need the total weight of the path, we don't have to bother keeping the path. We stop when we reach the bottom right node, and return the distances and the ending node.

The part one then just consist of calling the dijkstra:

def part_one(input_file: str):
    graph = get_graph(input_file)
    start_node = Node(0, 0, 3, Direction.EAST)
    distances, came_from, end = dijkstra(graph, start_node.copy())
    return distances[end] - graph.crucibles[-1][-1] + 1

I don't know why I needed to remove added one to the result, I just noticed it while playing with the example, but part 1 is solved !

Part 2

Rules

Part 2 is the same as part one, but we can now move 10 tiles in a straight line, and we need to move at least 4 tiles before turning.

Code

This is not too complicated to update. I chose to add minimum_steps and maximum_steps variables to the Graph class. I then have to update the advance method:

class Graph:
    def __init__(self, crucibles: list[list[int]], min_steps: int, max_steps: int):
        # ...
        self.min_steps = min_steps
        self.max_steps = max_steps

    # ...

     def advance(self, node: Node):
        # Return if no moves remaining
        if node.remaining_steps <= 0:
            return

        tmp_node = node.copy()
        weight = 0

        # If the node just rotated,
        # we need to advance the minimum numbers of steps first
        if tmp_node.remaining_steps == self.max_steps:
            for _ in range(self.min_steps):
                tmp_node.move()
                if self.out_of_map(tmp_node):
                    return
                weight += self.crucibles[tmp_node.y][tmp_node.x]
            yield tmp_node, weight

        # We then return each remaining step individually
        while tmp_node.remaining_steps > 0:
            tmp_node = tmp_node.copy()
            tmp_node.move()
            if self.out_of_map(tmp_node):
                return
            weight += self.crucibles[tmp_node.y][tmp_node.x]
            yield tmp_node, weight

We then have to change the initialization of the graph:

def part_two(input_file: str):
    min_steps, max_steps = 4, 10
    graph = get_graph(input_file, min_steps, max_steps)
    start_node = Node(0, 0, max_steps, Direction.EAST)
    distances, end = dijkstra(graph, start_node.copy())
    return distances[end]

And the part 2 is done !

Optimization

But it's so slow ! The solution takes almost 40 seconds to process the 2 parts:

python main.py 17  37.01s user 0.29s system 99% cpu 37.520 total

Let's see if we can make it faster. First, we start with a quick profiling:

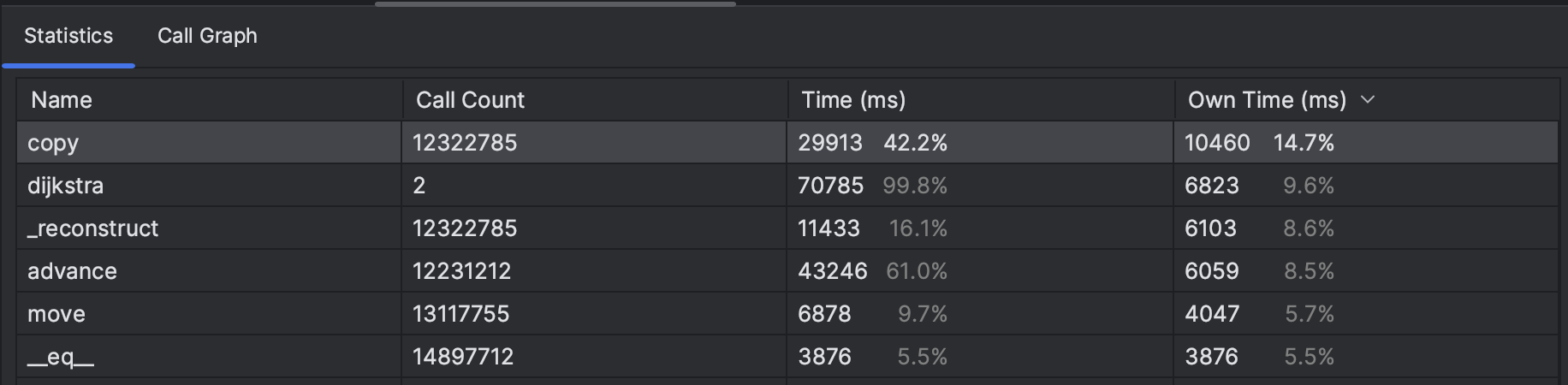
We can see that the call to copy is taking the most time. Let's have a look at this method again:

from copy import copy

class Node:
    # ...
    def copy(self):
        return copy(self)

To be fast, I used the implementation from the stdlib. Would implementing our own version make it faster ? Let's try with:

class Node:
    # ...
    def copy(self):
        return Node(self.y, self.x, self.remaining_steps, self.direction)

This is indeed way faster:

python main.py 17  25.10s user 0.18s system 99% cpu 25.319 total

Why ? I am not sure, but I would say it's because the copy function from the stdlib has to introspect each field of the object to create a copy, were our implementation is accessing each field directly.

This is still slow, but I think less than 30 seconds is enough for me, so let's call it a day !

---

All the code is available on github